説明
「フーリエ級数:正弦波による周期信号の合成」ページで言及した,Gibbs現象に関する補足説明です.
フーリエ級数において,加算項数を増やしていくと次第に元の信号波形に近づきますが,不連続(階段状の変化)がある波形に対しては,項数を増やしても不連続部分に突起状の乱れが残る,Gibbs現象が知られています. このページでは,「フーリエ級数:正弦波による周期信号の合成」のページに加え,上段左側の波形グラフの破線枠内を拡大したものを上段右側に表示しています.矩形波やのこぎり波のように波形に不連続がある場合,不連続部の前後で見られる突起と振動的な振る舞いは加算する正弦波の項数を増やしても小さくならず,時間方向を項数に応じて拡大すると,突起や振動的な振る舞いはほとんど変化しない様子が確認されます.
Gibbs現象がなぜ生じるかは,時間と周波数の双対性を考慮し,窓関数の知識を適用するとすっきり説明できます.フーリエ級数の正弦波加算を有限項数で打ち切ることは,周波数領域において矩形窓を乗算することに相当します.矩形窓のフーリエ(逆)変換は,sinc関数(\(\sin(x)/x\) の形)です.また,周波数領域での積は,時間領域での畳み込みと等価です.このため,時間領域では元の信号とsinc関数との畳み込みになります.sinc関数は中央の山の両側に正負に変動する波が存在し,その高さは中央の山の高さと比べて無視できない大きさです.このため,元の信号に階段状の変化があると階段状変化の前後で波状の挙動が生じます.
もう少し精密な話をすると,フーリエ級数で扱う周期信号の周波数成分は離散的ですので,加算を有限項数で打ち切ることは周波数領域で離散矩形信号をかけることに相当します.周波数領域の離散矩形信号を時間領域に変換すると,sinc関数を周期化した信号である,ディリクレ核 (Dirichlet kernel) になります.
フーリエ級数の第 \(N\) 項までで打ち切る場合,複素フーリエ級数で考えると \(-N\) から \(N\) までの間が1,それ以外が0という窓関数ですので,ディリクレ核はフーリエ級数の合成式により以下のように計算されます.
\(\quad
\begin{eqnarray}
\displaystyle
D_N(x)
&=& \sum_{k=-N}^N e^{jkx} \\
&=& 1 + \sum_{k=1}^N (e^{jkx} + e^{-jkx}) = 1 + 2 \sum_{k=1}^N \cos(kx) \\
&=& \frac{e^{-jNx}(1 - e^{j(2N+1)x})}{1-e^{jx}}
= \frac{e^{-jNx} e^{j(2N+1)x/2} (e^{j(2N+1)x/2} - e^{-j(2N+1)x/2})}{e^{jx/2}(e^{jx/2}-e^{-jx/2})}
= \frac{\sin((2N+1)x/2)}{\sin(x/2)}
\end{eqnarray}
\)
sinc関数とディリクレ核は,周期的かどうかの違いはあるものの,形状は非常によく似ています.\(N=10\) と \(N=100\) のディリクレ核とsinc関数を,それぞれ山の高さと振動の周期が一致するようスケーリングし重ねてプロットした図を示します.両者はグラフの端近くでの振幅に若干の違いがあるものの,ほとんど一致しています.
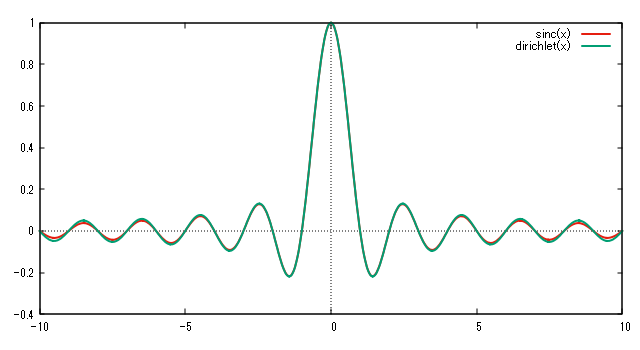
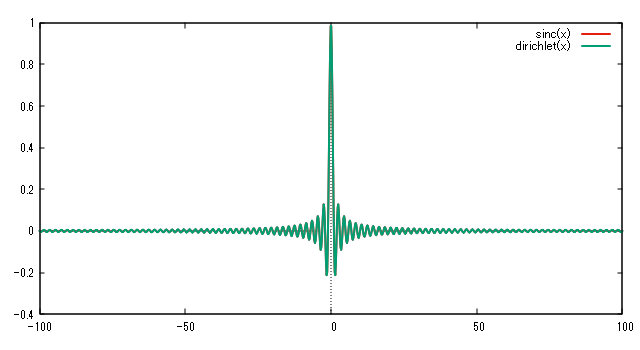
有限の項数で打ち切ったフーリエ級数により合成される信号は,周波数領域では元の信号のスペクトルと周波数領域における矩形窓との積なので,時間領域では元の信号波形(階段状)とディリクレ核との畳み込みになります.ここで注目すべきは,\(N\) の値を大きくすると,ディリクレ核はグラフの横(時間)方向に圧縮されますが,中央の山の両脇の振動の振幅はほとんど変化しないことです.このため,\(N\) の数を大きくする,すなわちフーリエ級数の加算項数を増やしたとき,不連続点付近での突起や振動的振る舞いは,グラフの横(時間)方向には縮まりますが縦(振幅)方向に小さくなることはありません.このため,フーリエ級数の加算項数を増やしても,項数が有限である限り不連続部での突起や振動的振る舞いは存在し続けます.
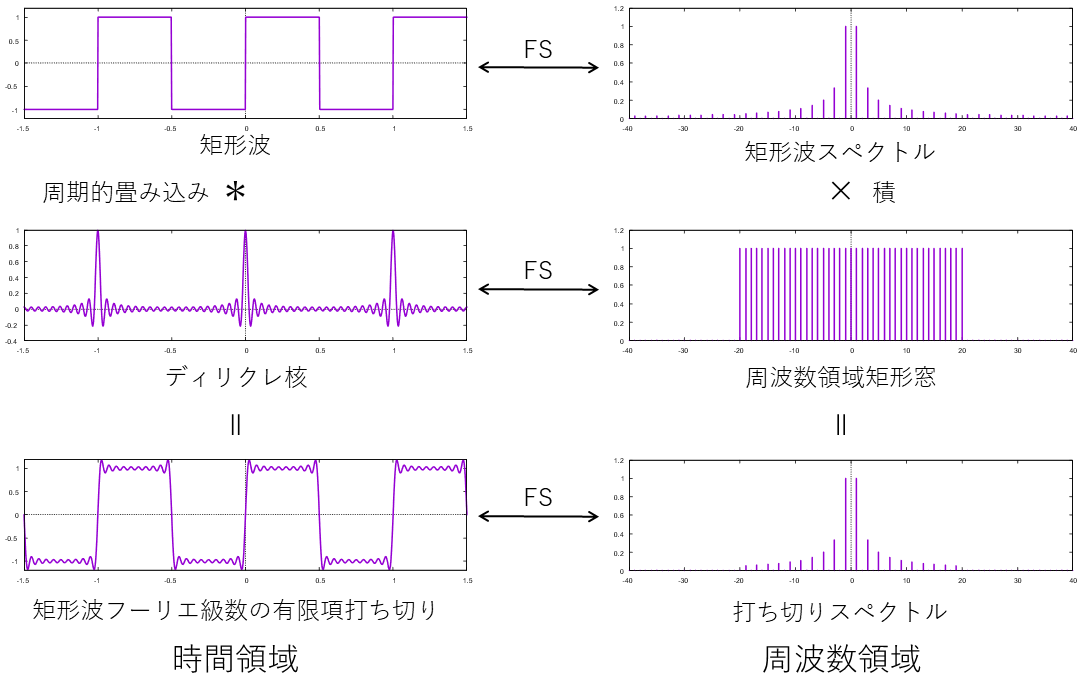
ここまでで,Gibbs現象はディリクレ核の波形が正負に振動することが原因とわかりました.ということは,フーリエ級数を有限項で打ちきるとき,等価的に時間領域で畳み込まれる信号(フーリエ核: Fourier kernel)が正負に振動しなければ,Gibbs現象は抑制されることが期待できます.そのためには,都合の良いフーリエ核に対応する周波数領域での重み(窓関数)を見つければよいことになります.通常の周波数解析において,窓関数は時間信号に乗算する形で使用されますが,ここでは時間と周波数の関係を逆転して,フーリエ級数係数に重みとして窓関数を乗算します.
前述のように有限項での単純な打ち切りは周波数領域において矩形窓をかけることであり,対応する時間領域でのフーリエ核は正負に振動するディリクレ核でした.突起や振動波形を発生させないためにはフーリエ核が非負であればよく,たとえばディリクレ核を2乗した形が該当します.時間領域での積は周波数領域での畳み込みですので,周波数領域では同じ矩形同士の畳み込み,すなわち三角形になります.ただし,正確にディリクレ核の2乗の効果を得ようとすると,周波数領域での窓長は2倍になり,より多くの項の加算を必要とします(単純打ち切りが,複素フーリエ級数で \(|k|\le N\) の範囲だとすると,周波数領域での三角窓は \(|k|\le 2N\) の範囲).このような,ディリクレ核の2乗に比例するフーリエ核は,フェイエール核 (Fejér kernel) と呼ばれます.他にも,いくつものフーリエ核が提案されています.
また,厳密に非負という制約を外せば,周波数解析で常用されるサイドローブの小さい窓関数,たとえばhann窓やhamming窓なども利用できます.これらを周波数領域での窓関数として利用すると,対応する時間波形は中央の山のみが残り両脇の振動的な振る舞いが同様に抑制されるとともに,サイドローブが三角窓よりも小さいため,振動的な振る舞いが軽減されるだけでなく,より本来の信号に近づくことが期待されます.
実際,「加算重み \(w_k\)」のラジオボタンを三角窓(Fejér核に対応),hann窓,hamming窓に指定すると,Gibbs現象による突起や振動的な振る舞いが著しく軽減されることが確認されます.ただし,これらの窓関数のメインローブ幅は同じ窓長の矩形窓よりも広いので,合成された時間信号の不連続点における変化は緩やかになります.オリジナルのフーリエ係数と重み付けされた係数の違いは,「スペクトル縦軸」をデシベル表記にするとわかりやすいでしょう.hann窓とhamming窓による効果の違いは,ほとんどわからないかもしれません.ごくわずかですが,不連続点両側のオーバーシュートはhamming窓の方が小さく,波形のリップルはhann窓の方が小さくなります.
hann窓やhamming窓の形状と,これらのサイドローブ高さが抑制される理由については,
が参考になると思います.
周期 \(T\) の周期信号のフーリエ級数:
\(\displaystyle\qquad
x(t) = \frac{a_0}{2} + \sum_{k=1}^\infty \left( a_k \cos\frac{2\pi kt}{T} + b_k \sin\frac{2\pi kt}{T} \right)
\)
フーリエ係数:
\(\displaystyle\qquad
\begin{eqnarray}
a_k &= \frac{2}{T} \int_0^T x(t) \cos\frac{2\pi kt}{T} dt \\
b_k &= \frac{2}{T} \int_0^T x(t) \sin\frac{2\pi kt}{T} dt \\
\end{eqnarray}
\)
信号波形とフーリエ係数:
| 信号波形 | フーリエ係数 | |
|---|---|---|
| 矩形波 | \(\displaystyle x(t)=\left\{ \begin{array}{cl} 1, & 0 \le t < 1/2 \\ -1, & 1/2 \le t < 1 \end{array} \right. \) | \(\displaystyle a_k = 0,\quad b_k = \left\{ \begin{array}{cl} \displaystyle \frac{4}{\pi k}, & k: {\rm 奇数} \\ 0, & k: {\rm 偶数} \end{array} \right. \) |
| のこぎり波 | \(\displaystyle x(t)=\left\{ \begin{array}{cl} 2t, & 0 \le t < 1/2 \\ 2t-2, & 1/2 \le t < 1 \end{array} \right. \) | \(\displaystyle a_k = 0,\quad b_k = \frac{2}{\pi k} (-1)^{k-1} \) |
| 三角波 | \(\displaystyle x(t)=\left\{ \begin{array}{cl} 4t, & 0 \le t < 1/4 \\ -4t+2, & 1/4 \le t < 3/4 \\ 4t-4, & 3/4 \le t < 1 \end{array} \right. \) | \(\displaystyle a_k = 0,\quad b_k = \left\{ \begin{array}{cl} \displaystyle \frac{8}{(\pi k)^2} (-1)^{(k-1)/2}, & k: {\rm 奇数} \\ 0, & k: {\rm 偶数} \end{array} \right. \) |
本ページにおける信号波形の例は,平均値(直流分)がゼロ,つまり \(a_0=0\) で,周期 \(T=1\) であり,かつ信号が奇関数のため \(a_k=0\) となる場合.
周波数領域での係数重みと対応する時間領域での関数:
\(\omega_0 = 2\pi/T\) として
| 係数重み(周波数領域窓関数) | 時間領域のフーリエ核 |
|---|---|
|
矩形窓(一定・単純打ち切り) \(\displaystyle\quad w_k = \left\{ \begin{array}{cl} 1, & |k| \le N \\ 0, & それ以外 \end{array} \right. \) |
Dirichlet核 \(\displaystyle D_N(\omega_0 t) = \frac{\sin((2N+1)\omega_0 t/2)}{\sin(\omega_0 t/2)} \) |
|
三角窓(矩形窓同士の畳み込み) \(\displaystyle\quad w_k = \left\{ \begin{array}{cl} \displaystyle 1 - \frac{|k|}{N}, & |k| \le N \\ 0, & それ以外 \end{array} \right. \) |
Fejér核(\(\approx\) Dirichlet核の2乗) \(\displaystyle \frac{1}{N}\cdot \frac{\sin^2((N+1)\omega_0 t/2)}{\sin^2(\omega_0 t/2)} \) |
|
コサイン窓(hann窓,hamming窓) \(\displaystyle w_k = \left\{ \begin{array}{cl} \displaystyle A + (1-A) \cos\frac{\pi k}{N}, & |k| \le N \\ 0, & それ以外 \end{array} \right. \) hann窓:\(A=0.5\) hamming窓:\(A=0.54\) |
Dirichlet核と,それを前後にずらしたものの和 \(\displaystyle AD_N(\omega_0 t)+\frac{1-A}{2} \left\{ D_N\left(\omega_0\left(t+\frac{T}{2N}\right)\right) + D_N\left(\omega_0\left(t-\frac{T}{2N}\right)\right) \right\} \) |
※ 冒頭のグラフでは,第\(N\)次高調波成分まで加算するという意味で,三角窓,hann窓における\(N\)次係数が非零となるよう \(N\) の代わりに \(N+1\) としています.