ディジタル信号処理の文脈でのフーリエ解析における時間と周波数の双対性の一例として,あまり多くの教科書では取り上げられていない「離散スペクトルからの連続スペクトル復元」を例示します.
離散時間信号の値を \(x[n]\) の欄に入力すると,その信号の
- 離散時間フーリエ変換 (DTFT) スペクトル(緑の曲線)
- 離散フーリエ変換 (DFT) スペクトル(赤の縦線)
- DFTスペクトルから内挿・復元した連続スペクトル(青の曲線)
- 周波数カーソルに最も近いDFTスペクトル値に対応する内挿スペクトル(オレンジの細線 )
を表示します.振幅と位相を計算したグラフと,カーソルが示す角周波数における値の複素平面上の位置を表示しています.DTFTスペクトルとDFTスペクトルから内挿した連続スペクトルは重ね描きしており(青の方が後),両者はわずかな計算誤差を除き一致していますので同じ曲線を描いているように見えますが,青い線の方は離散的なDFTスペクトルから内挿により連続スペクトルを復元したものです.離散時間信号からsinc関数内挿により連続時間信号を復元する場合と同様に,DFTの離散スペクトルから
周期的sinc関数の内挿によりDTFTの連続スペクトルを復元できる様子が確認できます.
このページでは,「短い離散時間信号の離散時間フーリエ変換 (DTFT)」と同様,非零の値が数点~20点程度の短い信号を扱っています.信号値入力欄では,非零の値を有するインデックス番号の範囲と,その範囲内の信号 \(x[n]\) の値を指定します.インデックス番号の範囲を変更すると,\(x[n]\) の入力欄の長さが変更されます.信号の値としては整数を入力するようになっています.DTFTスペクトルの計算においては,この範囲以外で \(x[n]=0\) と見なし,DFTスペクトルの計算では当該範囲を1周期分の信号と見なしています.この条件において,DFTスペクトルはDTFTスペクトルを周波数領域でサンプリングしたものになります.
DTFT: \(\displaystyle\quad X(e^{j\omega}) = \sum_{n=-\infty}^\infty x[n] e^{-j\omega n}
= \sum_{n=n_h}^{n_h+N-1} x[n] e^{-j\omega n}\)
DFT: \(\displaystyle\quad X[k] = \sum_{n=n_h}^{n_h+N-1} x[n] e^{-jk\omega_s n}\)
ただし,\(N\) は信号長(DFTではこれを信号周期と見なす),\(\omega_s = 2\pi/N\) はDFTスペクトルの正規化角周波数間隔,\(n_h\) は時間領域において信号1周期分の先頭となるサンプル番号です.
左右の矢印を押すと信号が1サンプルずつシフトします.このページではシフトにより左端または右端からはみ出した信号値が反対側へ循環します.ページを開いたときの初期値は,\(0\le n\le 4\) の5点が「1」でそれ以外が「0」の矩形信号です.「1」の範囲をシフトし区間の端にまたがる位置に持ってくると,「1」の区間が分断されるためDTFTの振幅スペクトルおよび復元された連続スペクトルは変化しますが,DFTではこの区間の周期信号と見なしているためDFTの振幅スペクトルは変化しません.
なお,連続スペクトル(DTFTスペクトル,内挿スペクトル)の計算は正規化角周波数で \(-\pi \le \omega \le \pi\) の範囲を800点に分割して行っています.値の絶対値がゼロに近いときは,atan2 で算出される位相の値に誤差が出る可能性があります.
ディジタル信号処理に関するほとんどの教科書において,連続時間信号の標本化と離散時間信号からの連続時間信号復元は説明されています.つまり,離散時間信号を生成する操作は,
-
時間領域では連続時間信号に標本化周期を間隔とするインパルス列を乗算する
-
周波数領域では元の信号の周波数スペクトルを標本化周波数ずつずらして複製(周期化)する
(=標本化周波数の間隔で並ぶインパルス列と畳み込む)
であり,離散時間信号から元の連続時間信号を復元する操作は,
-
時間領域ではsinc関数(矩形周波数スペクトルの逆フーリエ変換)で内挿する
(=sinc関数と離散時間信号(値つきインパルス列)を畳み込む)
-
周波数領域では周期化された周波数スペクトルのうち低周波側の1周期分を抽出する
=ナイキスト周波数を遮断周波数とする理想ローパスフィルタをかける
=±ナイキスト周波数を境界とする矩形スペクトルを乗算する
のように説明されています.
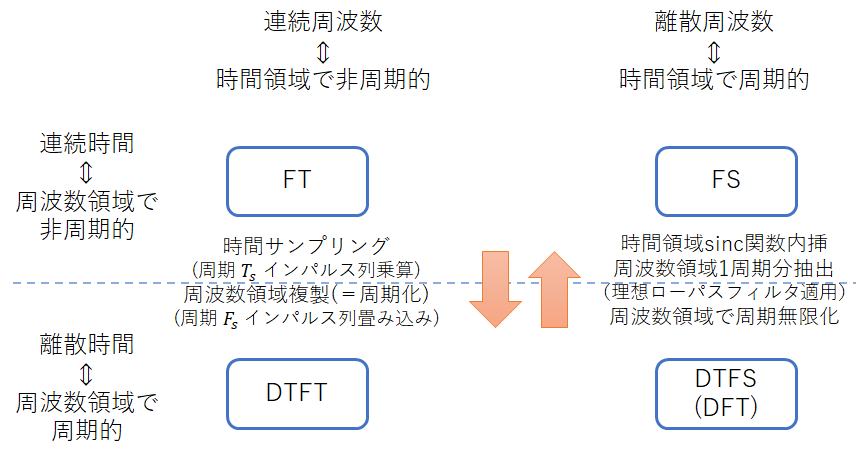
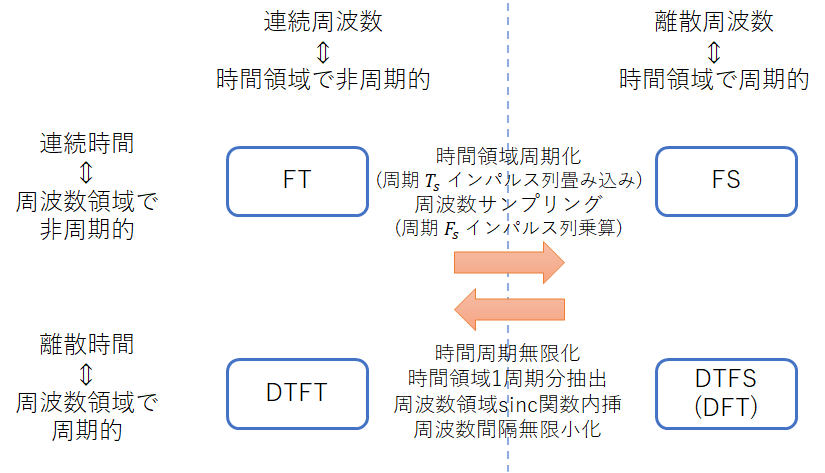
一方,上記のような連続時間信号と離散時間信号の関係が,時間と周波数の役割を入れ替えると,非周期信号(連続スペクトル)と周期信号(離散スペクトル)の関係にそのまま当てはまることを説明している教科書は,あまり多くないようです.つまり,連続スペクトルを周波数領域で標本化する操作は
-
時間領域では信号長ずつ時間をずらして複製(周期化)する
=信号長の間隔で並ぶインパルス列と畳み込む
-
周波数領域では連続スペクトルにスペクトル標本化周期を間隔とするインパルス列を乗算する
であり,逆に周期信号の離散スペクトルから連続スペクトルを復元する操作は
-
時間領域では周期化された信号から1周期分を抽出する
=1周期分は値が1,それ以外が0であるような矩形信号を乗算する
-
周波数領域ではsinc関数(連続時間矩形信号のフーリエ変換)または周期的sinc関数(離散時間矩形信号の離散時間フーリエ変換)で内挿する
=sinc関数(連続時間の場合)または周期的sinc関数(離散時間の場合)と離散スペクトル(値つきインパルス列)を畳み込む
であるという関係が存在します.これらの関係は,連続時間(フーリエ変換 (FT) とフーリエ級数 (FS)),離散時間(離散時間フーリエ変換 (DTFT) と離散時間フーリエ級数 (DTFS) / 離散フーリエ変換 (DFT))の双方で成立します.
このページでは,離散時間非周期信号の離散時間フーリエ変換 (DTFT) である連続スペクトルを周波数領域で標本化して得られる離散スペクトル(DFTスペクトル)の値から,周期的sinc関数を内挿することでDTFTの連続スペクトルが復元される様子を数値計算により検証しています.つまり,
-
有限長の信号のDTFTを計算し,連続スペクトルを得る
-
元の信号の長さ以上の整数を \(N\) とする.正規化角周波数の \(-\pi\sim+\pi\) の幅 \(2\pi\) の範囲を \(N\) 等分する角周波数で,周波数領域においてDTFTスペクトルを標本化したものがDFTスペクトル.このDFTスペクトルは,時間領域において信号を周期 \(N\) で周期化した周期信号の離散時間フーリエ級数 (DTFS) であるとも言える.
-
得られたDFTスペクトル(周波数に関して離散的)の値を用い,周波数領域において周期的sinc関数を内挿すると,元の連続スペクトルが復元される
という過程を示しています.なお,離散的なDFTスペクトルから連続スペクトルを復元する計算は,以下の式で行っています.
\(
\displaystyle\qquad
X(e^{j\omega}) =
\frac{1}{N} \sum_{k=0}^{N-1} X[k] \frac{\sin((\omega-k\omega_s)N/2)}{\sin((\omega-k\omega_s)/2)}
e^{-j(\omega-k\omega_s)(n_h+(N-1)/2)}
\)

